オイラーの公式
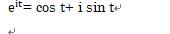
理系の大学初年度の学生ならば、必ず教わるオイラーの公式。私はそれを初めて目にした時に狐につままれたような気持ちになりました。
数式の意味について全く納得がいきませんでしたが、試験を突破する為にエイヤッと覚えて、とりあえず問題だけは解けるようにしていただけでした。
一般的にはe ^x、cos x 、sin xについて、それぞれマクローリン展開を行い、xにitを代入すると等式が成り立つ説明がなされ、無理やり分かったことにした人も多いでしょう。
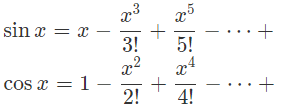
物理数学の直観的方法との出会い
しかしながら私は試験が終わった後でも頭にずっとひっかっかていました。もっと分かりやすい説明が無いものかと思い、大学生協の本屋に立ち寄ったところ、「物理数学の直感的方法」という本に巡り合いました。
そこには物理数学で必要となる公式についての図形を用いた視覚的、直感的説明がなされていました。この本のおかげで、テイラー展開、rotの公式などが、スーッと頭に入り、モヤモヤ感が一気に晴れました。
ざっくりとした解説
数式の意味についてザックリ説明します。複素数平面上でt=0の時はe itはe の0乗で1になります。ここで、皆が陥るトラップはtへさらに具体的な実数を代入しようとしてしまうことです。
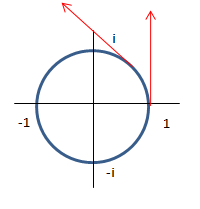
このように純粋にe^ itを検討していると絶対に理解出来ません。ここで軌跡を知るためにe itを微分します。そうするとie^ itとなります。iをかけているので、座標ベクトルを90度回転させたものが速度成分となります。そして座標とその軌跡の速度成分が、常に直交しているのは円しかありません
円軌跡
そうすると、e ^it = cos t + i sin tはe it の円軌跡を極座標表示しただけとなります。これよりe^ i π=ー1が何故成立しているかも視覚的に理解できるようになります。
つまり半径1の円の上を1から-1までπ時間かけて到達したということになります。(速度がie^ it=i(cost+i sint)なので、速度の絶対値は1です。そして、円周上の1から-1の軌跡上の距離はπ)